GNSS Spoofing Detection: Guard against automated ground vehicle attacks

RESULTS

We analyzed the proposed test statistics in both the non-spoofing case and against a worst-case attack, and present results with both the industrial- and consumer-grade IMUs.

Characterization of the Null Hypothesis. Our spoofing detector is premised on a hypothesis test between statistical models for the authentic and counterfeit GNSS signals. The statistics of the null hypothesis (no spoofing detected) must be fully characterized so that a statistical baseline is established, against which carrier-phase errors induced by spoofing in the same setting can be compared. The null hypothesis of dynamic ground vehicle scenarios includes natural effects such as blockage and multipath, which is the predominant source of error.

To analyze the null hypothesis, the WFARC was calculated in the nominal case through the entirety of the TEX-CUP dataset containing no spoofing. Because multipath is dependent on the surrounding environment, two categories were separately considered: shallow urban and deep urban. We separated measurements into these categories manually by identifying segments of the dataset where the vehicle resided in shallow urban and deep urban areas.

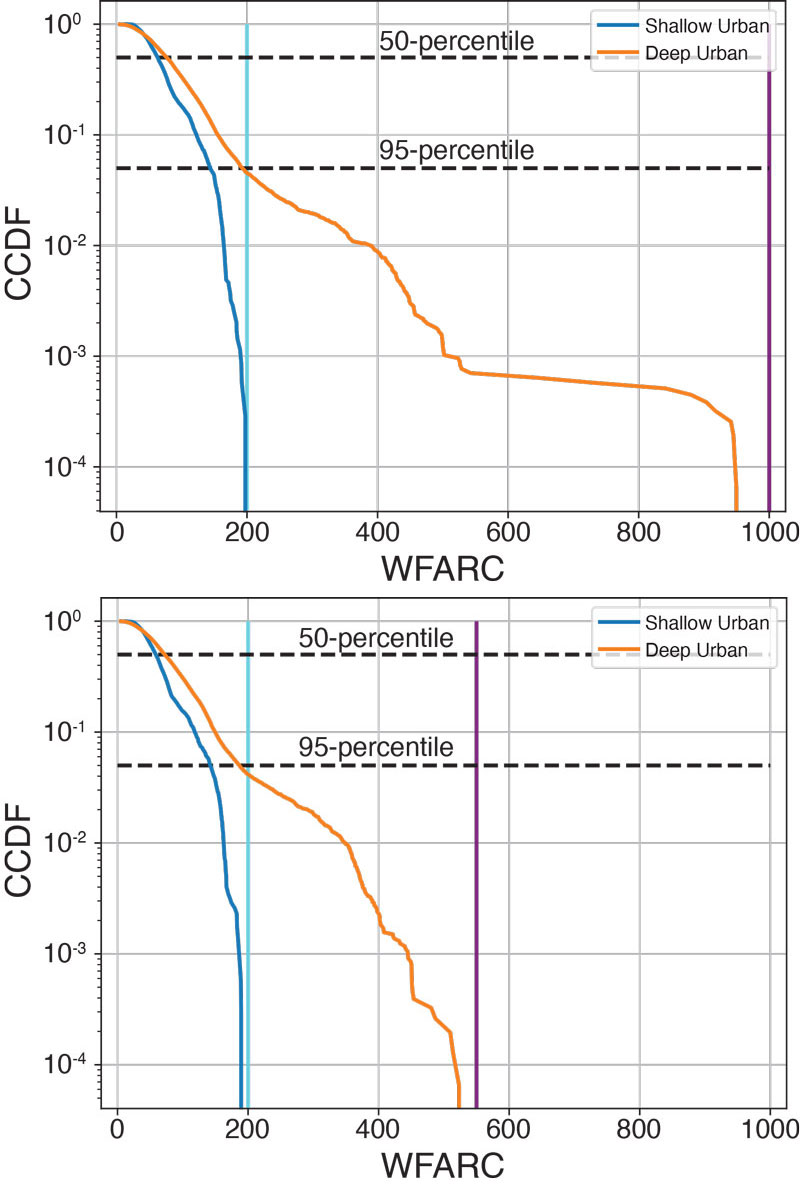
Figure 2: The complementary cumulative distribution function (CCDF) of the WFARC over the entire TEX-CUP dataset with the LORD MicroStrain 3DM-GX5-25 (industrial grade) IMU (top) and with the Bosch BMX055 (consumer grade) IMU (bottom).

Figure 2 shows the complementary cumulative distribution function (CCDF) of the WFARC in shallow and deep urban environments for the nominal case with industrial- and consumer-grade IMUs. The test statistic in the deep urban case has a much longer tail, which is expected because of the extreme multipath and blockage in deep urban areas. The cyan line represents the largest value of the WFARC in the shallow urban environment and the purple line represents the largest value of the WFARC in the deep urban environment. These will be the thresholds used to detect spoofing.

Because the test statistic in the null hypothesis is never larger than these values, it corresponds to having a false alarm probability of zero. A chi-squared test can be used to lower these thresholds but comes at the cost of having a fixed false positive rate. Figure 3 shows the time history of the WFARC over the TEX-CUP dataset.

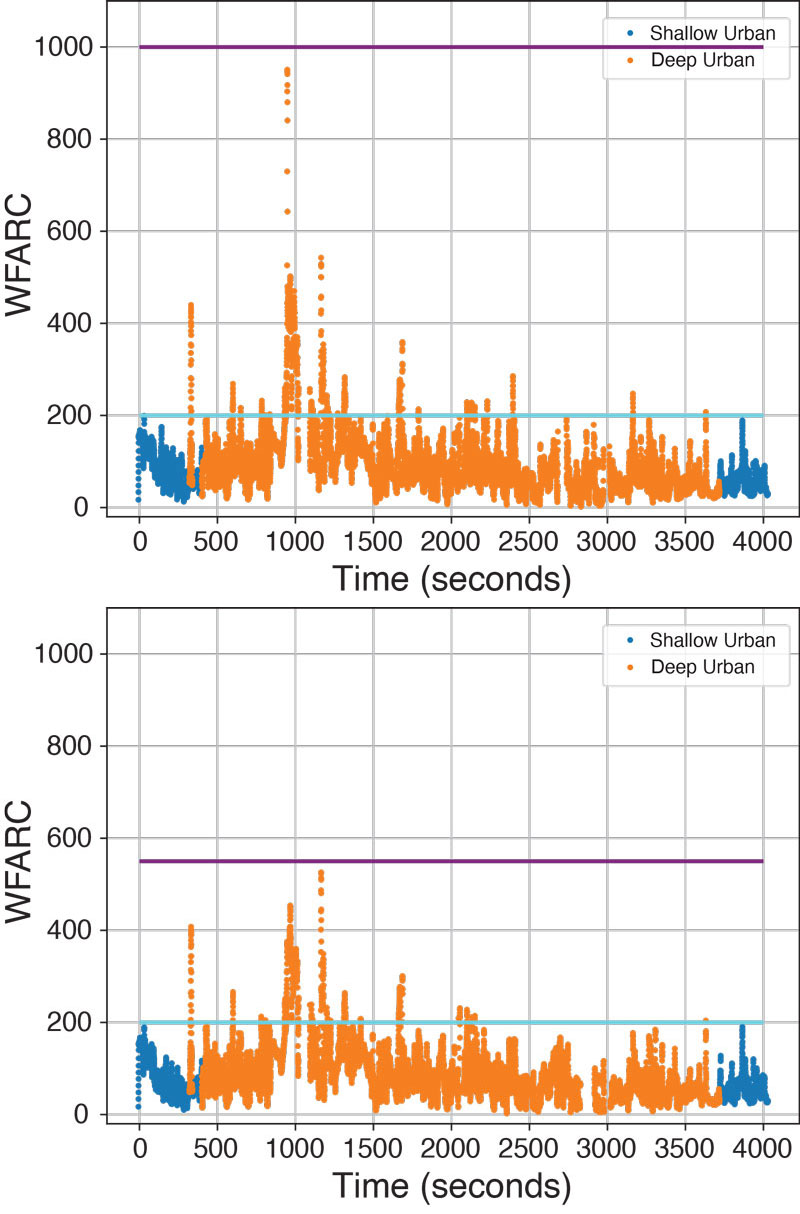
Figure 3: A time history of the WFARC over the entire TEX-CUP dataset with the industrial grade IMU (top) and the consumer grade IMU (bottom).

It is important to note that the WFARC while using the consumer-grade IMU is generally smaller than the WFARC while using the industrial-grade IMU. This is expected because the consumer-grade IMU is of lesser quality, thus having more variance with each measurement.

The a priori state estimate from IMU tight coupling has a larger uncertainty because the estimator has less confidence in the IMU measurements, leading corrupted measurements to be more believable. Once again, in the null hypothesis, spikes in the WFARC are caused by multipath and blockage.