The evolution of precise point positioning

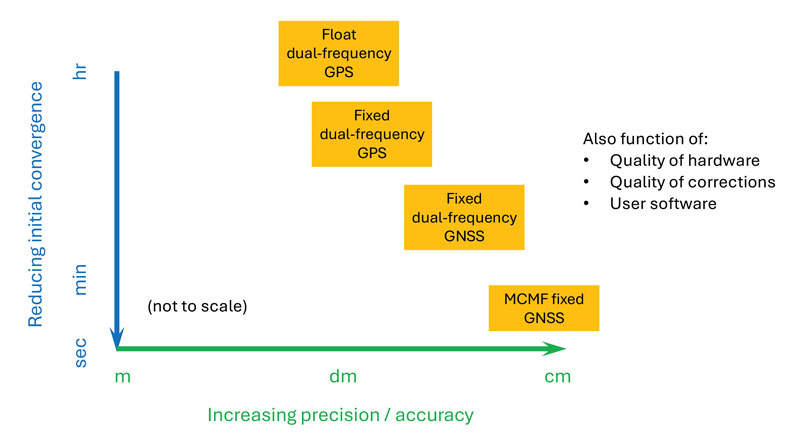 Figure 2: PPP and PPP-AR technology evolution in terms of accuracy versus convergence time.
Figure 2: PPP and PPP-AR technology evolution in terms of accuracy versus convergence time. Essence
Since the dawn of GPS, researchers have worked to improve the accuracy of estimated positioning, navigation and timing (PNT) from the receiver-derived pseudorange, carrier-phase and Doppler measurements. While the pseudorange-based accuracy of standard point positioning (SPP) at the level of 1s to 10s of meters sufficed for most users, carrier-phase-based relative positioning, real-time kinematic (RTK), network RTK (NRTK) and precise point positioning (PPP) measurement processing techniques were developed to provide decimeter-to-centimeter-level PNT under various constraints. Of these approaches, PPP — generally based on the state-space reduction of measurement errors to a single GNSS receiver from a wide area calibration network — has evolved dramatically. Why should readers read this article, as PPP has been around for some two decades? Well, some communities may consider old performance specifications of conventional/classical PPP, a rather niche technology, for static use with post-processing of measurements, resulting in tens of minutes for solution convergence to the decimeter level. However, there have been many performance advances, with more coming, affecting who uses the technology and how.
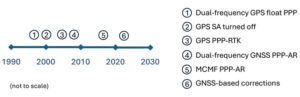
Figure 1 illustrates the timeline of PPP evolution, from:
- The development of the original technique in the late 1990s to reduce static GPS network measurement processing load.
- The removal of GPS Selective Availability (SA), simplifying precise satellite clock prediction.
- The development of PPP-RTK, in which regional RTK-derived corrections are used to reduce position convergence time and increase accuracy.
- Successful isolation of PPP GPS dual-frequency carrier-phase ambiguities to increase accuracy.
- Full multi-constellation, multi-frequency (MCMF) processing to greatly reduce position convergence time.
- The introduction of GNSS constellation provider corrections. (Individual advances will be discussed in the Elements section.)
From initial scientific uses to becoming the commercial standard in remote areas or regions with limited GNSS terrestrial infrastructure, these research contributions are leading to ubiquitous open sky decimeter to centimeter-level positioning with a range of available corrections, increasing accuracy and reducing initial convergence for more applications.
Essentials
In the late 1990s, to improve positioning accuracy over SPP and avoid the heavy computational burden of network-adjusted relative positioning processing between many receivers, PPP algorithms (detailed in the Elements section) were formulated with undifferenced measurements between tracked satellites and a single receiver (Zumberge et al. 1997). Both pseudorange and carrier-phase measurements are utilized, with the former presenting many decimeter-level references and the latter ambiguous centimeter-level ranging. By filtering continuously tracked measurements over time, decimeter- to centimeter-level positioning is possible, as the state terms, including real-valued estimates of biased carrier-phase ambiguity terms — resulting in tens of minutes to hours of initial convergence time. This approach represents Hatch filtering in the position state rather than the observation domain. Key to PPP is the use of precise satellite orbit and clock estimates derived from a global reference network, which can receive measurements from an entire GNSS constellation. Additionally, to maximize performance, remaining error sources are modeled or estimated. While PPP was initially not as accurate as RTK and, more importantly, took tens of minutes to hours to attain solution convergence, the technique did not have the terrestrial infrastructure constraints of RTK or network RTK, which require reference receivers ~10 km to 15 km and ~75 km away, respectively. Once GPS Selective Availability was turned off in 2000, GPS satellite clock modeling became simpler and more accurate, and scientific and commercial PPP solutions quickly became the standard measurement processing technique for applications requiring decimeter-level accuracy in remote areas or places where it was not economically viable to install (an) RTK base station(s).
In the 2000s, two different approaches were developed to deal with the shortcomings of PPP: PPP-RTK and PPP-AR. In PPP-RTK, state space corrections from a regional NRTK solution are efficiently transmitted and applied as PPP corrections. As NRTK resolves carrier-phase ambiguities and estimates local atmospheric (ionospheric and tropospheric) refraction and reference station position all in a least-squares sense, PPP-RTK can produce centimeter-level positioning in seconds within a reference station network, where stations can be tens to hundreds of kilometers apart. In PPP-AR, the ionosphere-free linear combination of dual-frequency pseudorange and carrier-phase measurements is not employed; rather, the uncombined version, and the pseudorange and carrier-phase observation models, are extended to include and isolate satellite and receiver fractional carrier-phase biases, allowing PPP ambiguity resolution (AR) to integers with additional satellite code and phase biases from the network solution and between satellite single-differencing. Both approaches are having significant scientific and commercial success.
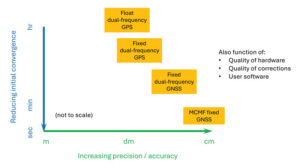
Unlike RTK, which has the benefit of significant additional calibration information from the reference station, PPP(-AR) must rely only on satellite-based corrections and the strength of the single-receiver observations. In recent years, additional GNSS constellation satellites and frequencies have been brought on-line in large numbers, and GNSS constellation-provided PPP corrections have begun (Xu et al. 2021; Fernandez-Hernandez et al. 2022; Naciri et al. 2023). These developments have greatly increased estimation redundancy, making near-instantaneous PPP without regional reference stations possible (Naciri and Bisnath 2023). This evolution of PPP technology in terms of positional accuracy versus convergence time is illustrated in Figure 2. Therefore, it may be possible to a) dissolve the old GNSS duality of niche, professional-grade versus mass-market, low-cost hardware and software with low-cost hardware utilizing PPP (and RTK and PPP-RTK) software countermeasures to obtain precise PNT; and b) with PPP corrections from GNSS constellations, perhaps, as a reversion to SPP, to have PPP be the natural operational mode of precise GNSS PNT (Bisnath 2020).
Elements
Theoretical development
The PPP measurement processing technique utilizes the GNSS pseudorange (code) and carrier-phase (phase) observables. For receiver r and satellite s, the respective code and phase measurements on frequency can be defined as:
where and Φi : pseudorange and carrier-phase measurements, respectively, in meters; ρ: geometric range between receiver and satellite; c: vacuum speed of light; dtr and dts: receiver and satellite clock offset from GPS Time, respectively; γi = ƒ ⁄ ƒ : ratio of frequencies applied to first frequency ionospheric delay I to recover ionospheric delay at frequency i; Tr : zenith troposphere wet delay; M: mapping function to map to satellite-receiver line-of-sight troposphere delay; λi = c ⁄ƒi: signal’s wavelength; N : integer ambiguity on frequency i; br,i and b: receiver and satellite pseudorange hardware biases, respectively; Br,i and B : receiver and satellite phase biases, respectively; and рi and Φi : residual unmodeled errors such as multipath and noise in code and phase measurements, respectively.where and Φi : pseudorange and carrier-phase measurements, respectively, in meters; ρ: geometric range between receiver and satellite; c: vacuum speed of light; dtr and dts: receiver and satellite clock offset from GPS Time, respectively; γi = ƒ ⁄ ƒ : ratio of frequencies applied to first frequency ionospheric delay I to recover ionospheric delay at frequency i; Tr : zenith troposphere wet delay; M: mapping function to map to satellite-receiver line-of-sight troposphere delay; λi = c ⁄ƒi: signal’s wavelength; N : integer ambiguity on frequency i; br,i and b: receiver and satellite pseudorange hardware biases, respectively; Br,i and B : receiver and satellite phase biases, respectively; and рi and Φi : residual unmodeled errors such as multipath and noise in code and phase measurements, respectively.
In order to eliminate ionospheric refraction, the original PPP solution forms the ionosphere-free (IF) linear combination of the dual-frequency GPS code and phase measurements:
From this combined form, the IF float PPP equations are (Kouba and Héroux 2001):
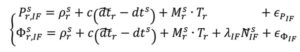
where the terms with tildes are biased by other terms from the starting observation equations, but allow for enough redundancy for user position, receiver clock offset, a zenith tropospheric term and real-valued, biased phase ambiguity terms to be estimated. In a sequential least-squares or Kalman filter optimal estimation process, positional accuracy depends on the quality of the satellite orbit and clock corrections, along with applying additional error modeling (including satellite and receiver antenna phase center offset and variation, solid Earth tides, ocean loading and phase wind-up), and, most importantly, the quantity, geometrical distribution and quality of the code and phase measurements. The state is initialized with m-level pseudorange measurements and slowly converges to the centimeter-level over tens of minutes to hours as the real-valued, biased phase ambiguity estimates reach steady state. This original or classic PPP solution, characterized by slow convergence to a fixed ambiguity-like positioning solution, may be what some in the community still think of as PPP.
PPP-RTK was developed as a means to remove these shortcomings of classical, float PPP by supplying PPP-like error state corrections from a regional RTK network to allow near-instantaneous carrier-phase ambiguity resolutionAR, (AR), solving both PPP’s convergence and accuracy problems (Wübbena et al. 2005). Significant operational improvements include increased spacing between (N)RTK reference stations, so less GNSS terrestrial infrastructure is required, and significant reduction in data transmissions from observation space representation (OSR) to state-space representation (SSR). By providing regional atmospheric corrections and ambiguity fixing, RTK-like performance is achieved but with larger CORS spacing. This approach has found commercial success in economically sustainable regions.
In parallel, active research continued in PPP-AR, given its desirable characteristic of not requiring regional reference stations. Multiple solutions were developed (e.g., Collins et al. 2008; Ge et al. 2008; Laurichesse et al. 2009), each of which reformulated the PPP observation equations to isolate the phase ambiguities, while overcoming datum defects in the estimation process. For example, the decoupled clock model (DCM) (Collins et al. 2008) isolates the phase ambiguities and directly estimates them as integers. The DCM does not make any assumptions regarding receiver biases and uses separate terms for code and phase clocks due to the imprecision in their synchronization — hence the model’s name. Satellite code and phase biases are required, along with satellite orbit and clock corrections. Then, standard AR methods, such as LAMBDA, can be applied. In the DCM, the fundamental code and phase equations are altered to:
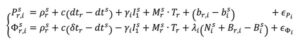
where dtr, and δtr, are the receiver code and phase clocks, respectively. The receiver pseudorange bias br,i is parameterized in such a way that it is grouped into the receiver pseudorange clock forming dtr and ionospheric delay forming I . These terms are derived to be:
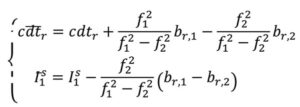
Through substitution, the DCM dual-frequency observation equations become:
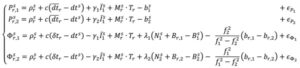
In decoupling the receiver clocks, the carrier-phase measurements lose their datum. To remove the estimation singularities, one satellite is selected as the reference satellite, its ambiguities are fixed to arbitrary integer values and used for between-satellite single-differencing. N = N + δN , where N are the arbitrarily set integer ambiguities on frequency i and δ N are the differences between the actual integer ambiguities and the arbitrarily set ones. Carrier-phase cycle slips must be detected and changes to the reference satellite accounted for. While initial solution convergence is still a characteristic of uncombined, dual-frequency PPP-AR, the uncombined model solved the problem of brief data outages (solution re-convergence), as the slant ionosphere estimates are used as a bridging parameter between small data gaps.
The dual-frequency model can be expanded to, e.g., quad-frequencies for multi-constellation, multi-frequency (MCMF) PPP-AR. Accounting for the use of a reference satellite per constellation, accounting for any spatial and temporal reference system differences between constellations, and additional inter-frequency pseudorange biases (IFBs) the up to quad-frequency DCM formulation can be derived as:
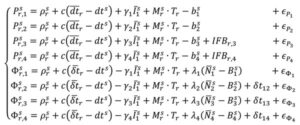
with:
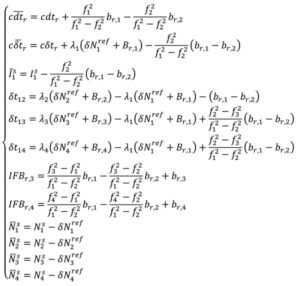
There is therefore the need for accurate and consistent MCMF satellite orbit, clock, code bias and phase bias corrections. Some constellation-based corrections, e.g., from QZSS, BDS and Galileo, are appearing.
There is therefore the need for accurate and consistent MCMF satellite orbit, clock, code bias and phase bias corrections. Some constellation-based corrections, e.g., from QZSS, BDS and Galileo, are appearing.
Results and analysis
How has PPP positioning solution convergence and accuracy evolved? The above model is now used to illustrate the performance of MCMF PPP-AR with up to four frequencies. The quad-frequency model has been implemented in the York-PPP client engine developed at York University. For performance illustration purposes, Centre national d’études spatiales (CNES) MCMF correction products are used for consistency and one day (day of year 128 in 2024) of high-quality MCMF GNSS observations are used from each International GNSS Service (IGS) stations CUSV in Bangkok, Thailand, KIR8 in Kiruna, Sweden, and RABT in Rabat, Morocco. Note that data from other days and other comparable stations produce similar positioning results. Simulated real-time, sequential least-squares, kinematic processing was performed for the following observation scenarios: 1) dual-frequency GPS (dual G); 2) dual-frequency GPS and GLONASS (float), with no ambiguity fixing of the frequency-division, multiple access GLONASS signals (dual GR); 3) dual-frequency GPS, GLONASS and Galileo (dual GRE); 4) dual-frequency GPS, GLONASS (float), Galileo and BeiDou (dual GREC); 5) up to triple-frequency GPS, dual-frequency GLONASS (float), triple-frequency Galileo and triple-frequency BeiDou (triple GREC); and 6) up to triple-frequency GPS, dual-frequency GLONASS (float), quadruple-frequency Galileo and quadruple-frequency BeiDou (quad GREC). Operational effects, such as correction latency, are not considered. Figure 3 demonstrates MCMF PPP-AR horizontal error initial solution convergence for these scenarios, averaged from each 24-hour dataset, reset every three hours across the three global stations.
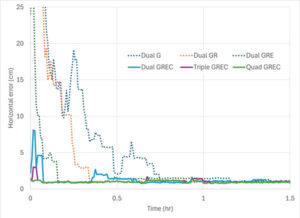
The dashed time series in figure show the benefits of adding constellations in the PPP-AR processing. From the average of the dual-frequency GPS solutions, the addition of each constellation reduces convergence time by approximately one-half. Then, by adding additional frequencies, convergence time is further reduced to basically instantaneous convergence using available measurements on up to four frequencies from all four GNSS constellations. These results bode well for GNSS data collection in sky-obstructed areas or with lower-quality hardware. Figure 4 provides the convergence times for the average solutions from each processing scenario to reach and sustain below 10 cm and 2.5 cm horizontal error, respectively. These are typical specifications for numerous static and kinematic applications. Four constellation, dual-frequency data are required to attain 10 cm horizontal positioning error or better near-instantaneously. However, to achieve the 2.5 cm convergence definition, at least triple-frequency data are necessary. The post-10 cm convergence horizontal solution accuracy, as defined by rms error, is 9 cm for dual-frequency GPS and 1 cm for each of the GREC processing scenarios. The post-2.5 cm convergence horizontal solution accuracy, as defined by rms error is 17 cm for dual-frequency GPS and 4 cm for each of the GREC processing scenarios.

What if a more robust PPP solution is considered that also further analyzes the introduction of additional frequencies? The same three-station, one-day dataset can be processed in an epoch-by-epoch mode, where all filter states are reset. Therefore, there is no filtering with no assumptions about system dynamics. In this case, using a 30-second sampling rate, results in 8,640 position estimate “snapshots” — a robust process of estimation that can be useful for, e.g., clearly defining integrity for safety-of-life applications. The MCMF PPP-AR results for 1) dual-frequency GPS, GLONASS (float), Galileo and BeiDou (dual GREC); 2) up to triple-frequency GPS, dual-frequency GLONASS (float), triple-frequency Galileo and triple-frequency BeiDou (triple GREC); and 3) up to triple-frequency GPS, dual-frequency GLONASS (float), quadruple-frequency Galileo and quadruple-frequency BeiDou (quad GREC). Figure 5 illustrates the epoch-by-epoch horizontal positioning performance (in cm) for these three scenarios using planimetric subplots. Most position estimates for each scenario are near each subplot center. Adding measurements from the additional frequencies from the dual-frequency base to up to three frequencies and then up to four frequencies for the same four constellations greatly improves horizontal positioning precision and greatly reduces the quantity and magnitude of positioning outliers.
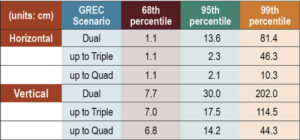
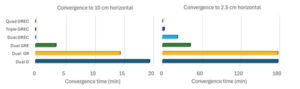
Table 1 provides the epoch-by-epoch MCMF GNSS PPP-AR horizontal and vertical 68th (1-sigma), 95th (2-sigma) and 99th (3-sigma) percentile positioning error statistics for the same dataset. At the 68th percentile, all scenarios produce centimeter-level horizontal and sub-decimeter-level vertical positioning. However, at the 95th percentile, only triple- and quad-frequency processing can produce centimeter-level positioning in the horizontal component and near decimeter-level positioning in the vertical. To assess extreme position estimate outliers, the 99th percentile statistics show that dm-level horizontal positioning can be maintained with quad-frequency processing.

The MCMF PPP-AR filtered results indicate that near-instantaneous, cm-level PPP is achievable with quality geodetic observations. The epoch-by-epoch, unfiltered results imply that robust, centimeter-level PNT is achievable. Table 2 provides the average redundancy in the epoch-by-epoch processing, where the redundancy is the difference between the number of measurements used and the estimation states. This measure provides insight to how the increase in the number of measurements, while not increasing the number of satellites or the dilution of precision, significantly improves PNT estimation performance for PPP-AR — as this is a measurement-driven technique. The average redundancy increases from 34 to 62 when expanding from dual-frequency GPS to dual-frequency GPS + Galileo and to 121 when using dual-frequency measurements from all constellations. Additionally, increasing processing to include up to triple-frequency measurements and quad-frequency measurements grows this metric to 154 and 183, respectively. The estimation process then becomes more robust against measurement errors and biases. It has more measurement strength to estimate all state parameters, including slant ionosphere refraction terms and integer ambiguities, allowing for improved position estimation precision.
Evolutionary
MCMF PPP-AR performance continues to improve. Positioning performance for quality geodetic measurements can produce horizontal centimeter-level positioning performance nearly instantaneously. Robust performance can be obtained with epoch-by-epoch processing, resulting in centimeter-level and few-centimeter-level horizontal and vertical positioning at the 95th percentile level using up to quadruple frequency measurements. Also, inclusion of additional measurements from additional frequencies greatly improves estimation redundancy, thereby improving state estimation.
Future research developments, testing and implementation include: adding measurements from available fifth frequencies; investigating less reliance on noisy and multipath-prone pseudorange measurements; expanding robust near-instantaneous PPP in urban environments; further defining/characterizing PPP integrity and safety integrity levels; having PPP be an independent or complimentary solution to/with (N)RTK for precise PNT; minimize requirements for atmospheric corrections; further use of PPP in mass-market hardware; and further integration of PPP as part of sensor suite solutions (e.g., automotive, smartphone, UAV, robotics, etc.) for resilient PNT.
Finally, what is the usefulness of the research in our lives? PPP measurement processing for GNSS is the scientific and industry standard for many user applications. There continues to be growing commercial adoption of this evolving technology, including expanded use in traditional (N)RTK precise applications, mass-market applications using low-cost hardware, and safety-of-life applications, including automotive, other passenger vessels, smartphones, robotics, UAVs and for aids to pedestrians.
















Follow Us